Understanding the Decimal Representation of 1/10

Understanding the decimal representation of 1⁄10 is a fundamental concept in mathematics that bridges the gap between fractions and decimals. This simple fraction, when converted to a decimal, becomes 0.1, a value we encounter daily in various contexts, from financial transactions to scientific measurements. Grasping this conversion not only strengthens your mathematical foundation but also enhances your ability to work with numbers in real-world scenarios. Whether you’re a student, a professional, or simply curious about numbers, this guide will walk you through the process and significance of representing 1⁄10 as a decimal.
What is the Decimal Representation of 1⁄10?

The decimal representation of 1⁄10 is 0.1. This means that one-tenth of a whole is equivalent to 0.1 in decimal form. The conversion is straightforward: divide 1 by 10, and the result is 0.1. This value is essential in decimal systems, as it forms the basis for understanding tenths, hundredths, and beyond.
📌 Note: The decimal 0.1 is a terminating decimal, meaning it has a finite number of digits after the decimal point.
How to Convert 1⁄10 to a Decimal

Converting 1⁄10 to a decimal involves a simple division process. Here’s a step-by-step breakdown:
- Set Up the Division: Write 1 as the dividend and 10 as the divisor.
- Perform the Division: Divide 1 by 10.
- Write the Result: The quotient is 0.1.
This method highlights the relationship between fractions and decimals, making it easier to visualize and understand.
Why is 0.1 Important?
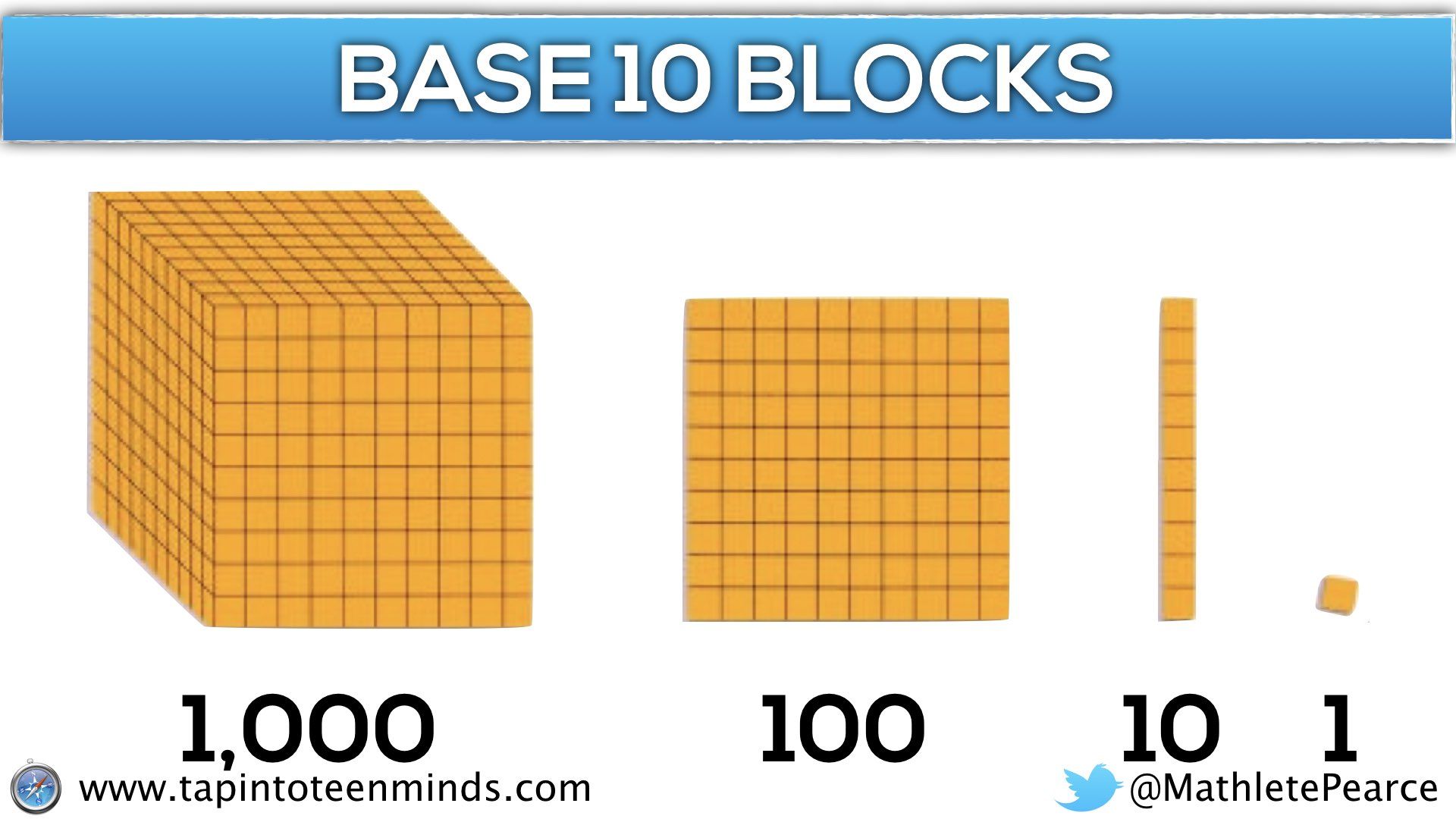
0.1 is a cornerstone in the decimal system, serving as the foundation for higher decimal places. For instance:
- 0.1 represents one-tenth.
- 0.01 represents one-hundredth.
- 0.001 represents one-thousandth.
Understanding 0.1 helps in comprehending place value, which is crucial for advanced mathematical operations like addition, subtraction, multiplication, and division of decimals.
Practical Applications of 0.1

The decimal 0.1 is widely used in everyday life. Here are some practical examples:
- Finance: Calculating 10% discounts or taxes.
- Cooking: Measuring ingredients like 0.1 liters of water.
- Science: Representing data in graphs or charts.
| Application | Example |
|---|---|
| Finance | 10% discount on a $10 item = $1.00 |
| Cooking | 0.1 kg of flour in a recipe |
| Science | 0.1 grams of a chemical in an experiment |

Checklist for Mastering 0.1

To solidify your understanding of 0.1, follow this checklist:
- Practice Conversion: Convert 1⁄10 to a decimal multiple times.
- Explore Place Value: Understand how 0.1 relates to 0.01 and 0.001.
- Apply in Real Life: Use 0.1 in daily calculations.
- Test Yourself: Solve problems involving 0.1 in different contexts.
In summary, the decimal representation of 1⁄10 as 0.1 is a basic yet powerful concept in mathematics. It serves as the building block for understanding decimals and their applications in various fields. By mastering this conversion, you enhance your numerical literacy and gain confidence in handling more complex mathematical tasks.
What is the decimal representation of 1/10?
+The decimal representation of 1/10 is 0.1.
Why is 0.1 important in mathematics?
+0.1 is important because it represents one-tenth and serves as the foundation for understanding higher decimal places like hundredths and thousandths.
How can I practice converting fractions to decimals?
+Practice by converting simple fractions like 1/2, 1/5, and 1/10 to decimals and gradually move to more complex fractions.
decimal representation, fraction to decimal conversion, mathematical concepts, decimal system, numerical literacy.


