Domain Composition of Functions Explained Simply
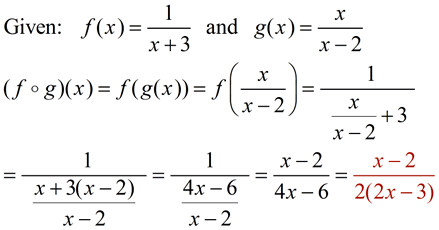
Understanding the domain composition of functions is essential for anyone studying mathematics or applying it in real-world scenarios. This concept simplifies complex problems by breaking them down into manageable parts, making it a cornerstone in fields like calculus, computer science, and engineering. Whether you're a student, educator, or professional, mastering this topic will enhance your problem-solving skills and mathematical fluency.
What is Domain Composition of Functions?

The domain composition of functions, often denoted as ( f \circ g ), involves applying one function to the output of another. Mathematically, if ( f(x) ) and ( g(x) ) are two functions, their composition is defined as ( (f \circ g)(x) = f(g(x)) ). The domain of this composition is the set of all inputs ( x ) for which ( g(x) ) is defined and lies within the domain of ( f ).
📌 Note: The domain of ( f \circ g ) is more restrictive than the domains of ( f ) and ( g ) individually.
How to Determine the Domain of Composite Functions

To find the domain of ( f \circ g ), follow these steps:
- Step 1: Identify the domains of ( f ) and ( g ). Ensure you know the valid inputs for both functions.
- Step 2: Find the range of ( g ). This will help determine which outputs of ( g ) can be inputs for ( f ).
- Step 3: Ensure ( g(x) ) is within the domain of ( f ). The domain of ( f \circ g ) includes only ( x ) values where ( g(x) ) is defined and falls within ( f )’s domain.
📌 Note: Always check for restrictions like division by zero or square roots of negative numbers.
Practical Applications of Domain Composition

The domain composition of functions is not just a theoretical concept; it has real-world applications:
- Data Transformation: In data science, composing functions helps preprocess and transform data efficiently.
- Physics and Engineering: Composite functions model complex systems by breaking them into simpler components.
- Computer Programming: Functions are composed to create modular and reusable code.
Common Mistakes to Avoid

When working with domain composition of functions, avoid these pitfalls:
- Ignoring Domain Restrictions: Failing to check if ( g(x) ) is in ( f )’s domain can lead to incorrect results.
- Misinterpreting Composition Order: Remember, ( f \circ g ) is not the same as ( g \circ f ).
- Overlooking Edge Cases: Test boundary values to ensure the composition is defined for all intended inputs.
Checklist: Mastering Domain Composition

- Understand the individual domains of ( f ) and ( g ).
- Verify that ( g(x) ) falls within the domain of ( f ).
- Practice with diverse examples to reinforce your understanding.
- Apply composition in real-world problems to see its practical value.
By now, you should have a clear understanding of the domain composition of functions. This concept is a powerful tool in mathematics and beyond, enabling you to tackle complex problems with confidence. Keep practicing, and soon you’ll master this essential skill.
What is the domain of a composite function?
+The domain of a composite function ( f \circ g ) is the set of all ( x ) values for which ( g(x) ) is defined and lies within the domain of ( f ).
Can the composition of functions be commutative?
+No, function composition is generally not commutative. ( f \circ g ) is typically different from ( g \circ f ).
How do I handle restrictions in composite functions?
+Always check for restrictions like division by zero, square roots of negative numbers, or values outside the domain of either function.


