Understanding the Equality Property of Multiplication: Key Concepts Simplified

Understanding the equality property of multiplication is essential for mastering algebra and solving complex equations. This fundamental concept allows us to manipulate expressions and isolate variables with ease. Whether you're a student, educator, or simply looking to refresh your math skills, this guide breaks down the key concepts into digestible, actionable insights. From its definition to practical applications, we’ll explore everything you need to know to confidently apply the equality property of multiplication in various scenarios, (algebraic properties, multiplication rules, math fundamentals)

What is the Equality Property of Multiplication?

The equality property of multiplication states that if you multiply both sides of an equation by the same non-zero number, the equality remains unchanged. Mathematically, if ( a = b ), then ( a \times c = b \times c ) for any non-zero value of ( c ). This property is a cornerstone in algebra, enabling us to solve equations systematically. It ensures that the balance of an equation is maintained, making it a reliable tool for problem-solving, (equation balancing, algebraic principles, math properties)

Why is the Equality Property Important?

The equality property of multiplication is crucial for several reasons:

• Solving Equations: It allows us to isolate variables in equations.
• Maintaining Balance: Ensures the equation remains true after operations.
• Versatility: Applies to various mathematical and real-world problems.

Mastering this property opens doors to advanced mathematical concepts and applications, (problem-solving, equation isolation, mathematical balance)

How to Apply the Equality Property of Multiplication

Applying the equality property involves a straightforward process:

1. Identify the Equation: Start with an equation where both sides are equal.
2. Multiply Both Sides: Multiply both sides by the same non-zero number.
3. Simplify: Simplify the equation to solve for the variable.

For example, if ( x = 5 ), then ( x \times 2 = 5 \times 2 ), resulting in ( 2x = 10 ). This method is particularly useful in linear equations, (equation application, step-by-step math, linear equations)

📌 Note: Always ensure the multiplier is non-zero, as multiplying by zero would make both sides of the equation zero, which is not helpful for solving equations.

Practical Examples of the Equality Property

Let’s explore some examples to solidify understanding:

Equation	Multiplied By	Result
( x = 4 )	3	( 3x = 12 )
( y = 7 )	2	( 2y = 14 )

These examples demonstrate how the property preserves equality while scaling both sides of the equation, (math examples, equation scaling, practical math)

Common Mistakes to Avoid

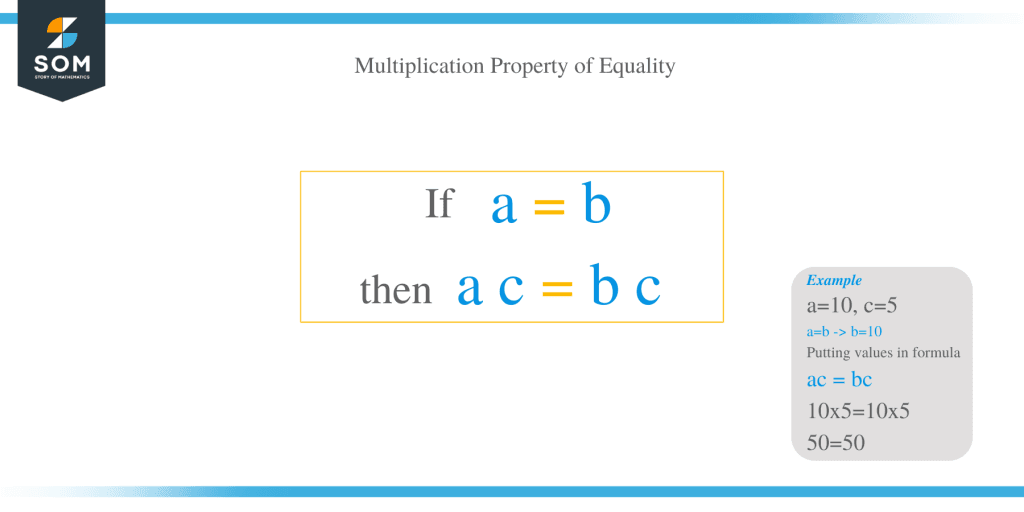
When working with the equality property, be mindful of:

• Multiplying by Zero: This results in both sides being zero, which is unhelpful.
• Forgetting to Multiply Both Sides: Only multiplying one side disrupts the equation’s balance.
• Ignoring Non-Zero Requirement: Always ensure the multiplier is non-zero.

Avoiding these pitfalls ensures accurate and efficient problem-solving, (common math errors, equation balance, problem-solving tips)

The equality property of multiplication is a powerful tool in algebra, enabling us to solve equations with precision and confidence. By understanding its definition, importance, and application, you can tackle a wide range of mathematical problems. Remember to always multiply both sides by a non-zero number and avoid common mistakes to maintain the equation’s balance. With practice, this property will become second nature, enhancing your mathematical skills and problem-solving abilities, (algebraic tools, math confidence, equation solving)