Parametric Equation for a Circle: Simplified Guide
<!DOCTYPE html>
Understanding the parametric equation for a circle is essential for anyone diving into geometry, calculus, or computer graphics. This guide breaks down the concept into simple, actionable steps, making it accessible for both students and professionals. Whether you're plotting circles in coordinate geometry or applying them in mathematical modeling, this post will equip you with the knowledge you need.
What is the Parametric Equation for a Circle?

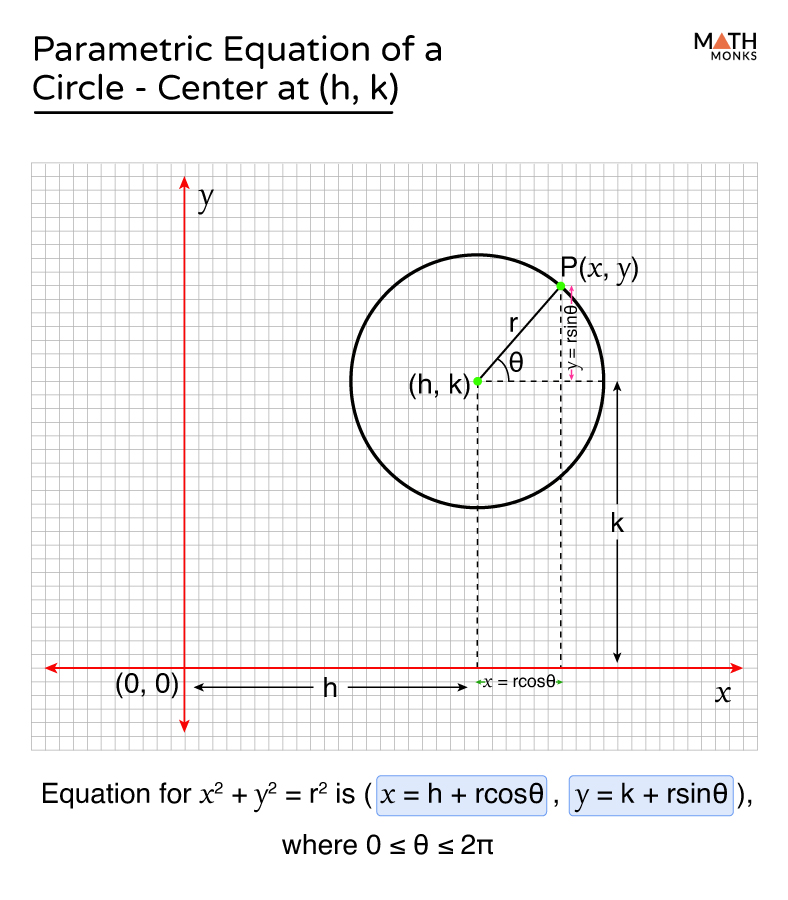
The parametric equation for a circle represents a circle in terms of a parameter, typically denoted as ( t ). Unlike the standard Cartesian equation ( x^2 + y^2 = r^2 ), parametric equations express ( x ) and ( y ) as separate functions of ( t ). This approach is particularly useful in animation, engineering, and physics, where motion along a circular path needs to be described dynamically.
Deriving the Parametric Equations
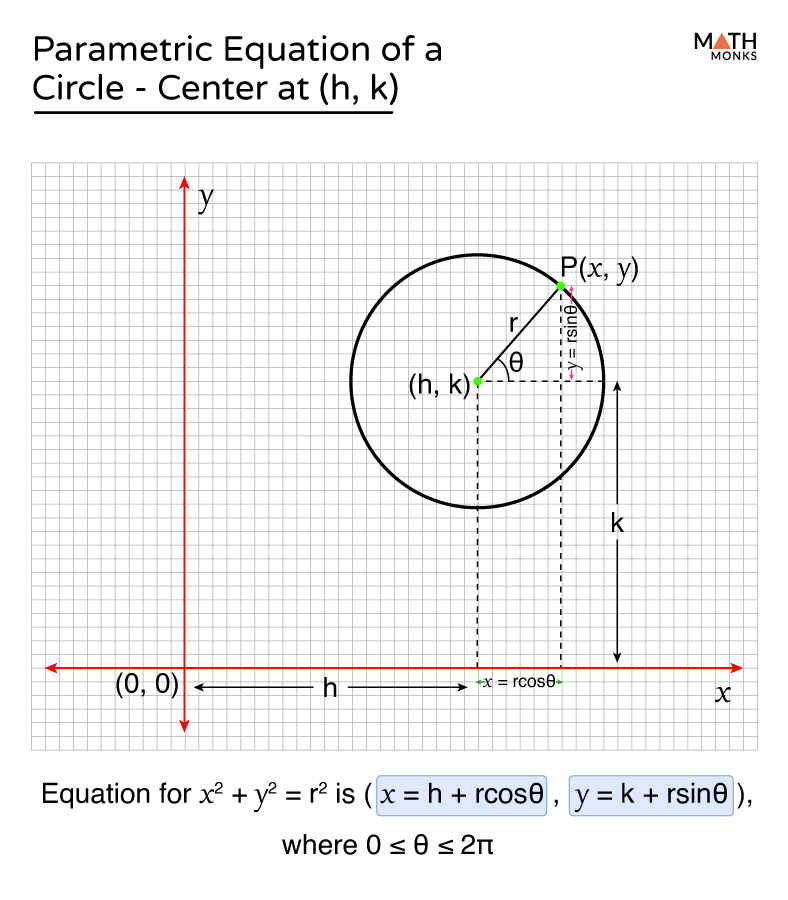
The parametric equations for a circle centered at the origin with radius ( r ) are:
- ( x = r \cos(t) )
- ( y = r \sin(t) )
Here, ( t ) varies from ( 0 ) to ( 2\pi ) to trace the entire circle. These equations are derived from the unit circle definitions of sine and cosine, scaled by the radius ( r ).
Applications of Parametric Equations
Parametric equations are not just theoretical; they have practical applications in:
- Computer Graphics: Animating objects moving in circular paths.
- Engineering: Modeling circular motion in machinery.
- Physics: Describing planetary orbits or pendulum swings.
Step-by-Step Guide to Plotting a Circle Using Parametric Equations

- Define the Radius: Choose the radius ( r ) of the circle.
- Set Up Parameters: Use ( t ) ranging from ( 0 ) to ( 2\pi ).
- Calculate Coordinates: Compute ( x = r \cos(t) ) and ( y = r \sin(t) ) for each ( t ).
- Plot the Points: Graph the ((x, y)) pairs to visualize the circle.
📌 Note: Ensure t is incremented in small steps for smoother plotting.
Checklist for Working with Parametric Equations

- Understand the role of the parameter ( t ).
- Use trigonometric functions correctly for ( x ) and ( y ).
- Verify the range of ( t ) for a complete circle.
- Apply the equations in practical scenarios like animation or modeling.
Mastering the parametric equation for a circle opens doors to advanced mathematical and technical applications. By following this guide, you’ll gain a solid foundation in this fundamental concept, parametric equations,circle geometry,mathematical modeling.
What is the parametric equation for a circle?
+The parametric equations for a circle centered at the origin with radius r are x = r \cos(t) and y = r \sin(t) , where t is the parameter.
Why use parametric equations instead of the standard equation?
+Parametric equations are useful for describing motion or paths dynamically, making them ideal for applications in animation, engineering, and physics.
How do I plot a circle using parametric equations?
+Define the radius, set up the parameter t , calculate x and y using the parametric equations, and plot the points for each t value.



