Understanding the Taylor Series for 1/x: A Simple Guide

The Taylor Series is a powerful mathematical tool used to represent functions as infinite sums of their derivatives. One of the most intriguing applications is the Taylor Series for 1/x, which provides deep insights into function behavior around a point. Whether you're a student, researcher, or simply curious about advanced mathematics, understanding this series can unlock new perspectives in calculus and analysis. In this guide, we’ll break down the concept step-by-step, making it accessible even for beginners. (Taylor Series Expansion, Calculus Fundamentals)
What is the Taylor Series for 1/x?

The Taylor Series for 1/x is an infinite series representation of the function ( f(x) = \frac{1}{x} ) around a point ( a \neq 0 ). It’s derived using the Taylor Series formula, which expresses a function as a sum of its derivatives evaluated at a specific point. For ( 1/x ), the series is particularly interesting because it involves negative powers of ( (x - a) ). (Taylor Series Formula, Infinite Series)
Deriving the Taylor Series for 1/x
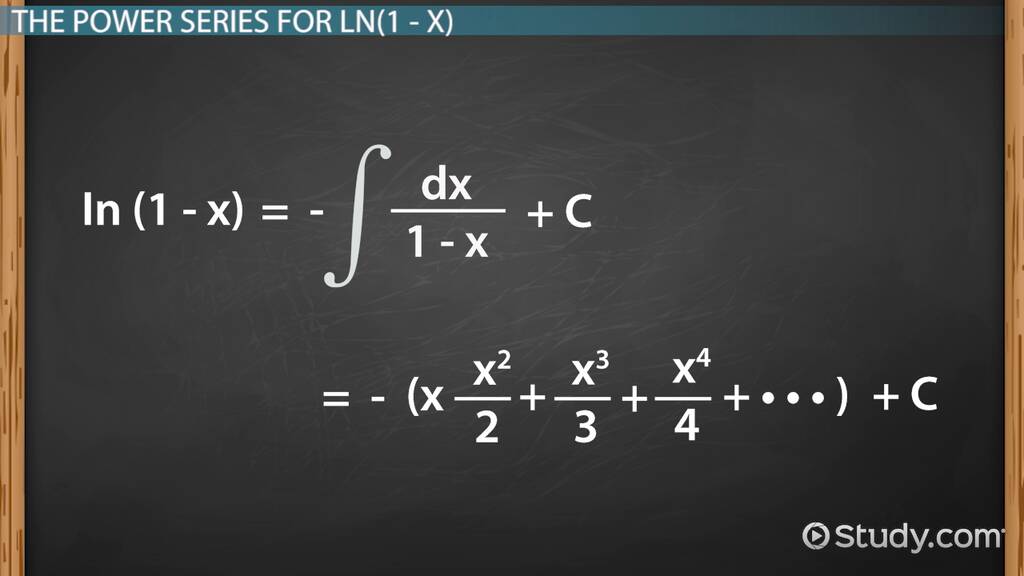
To derive the Taylor Series for ( 1/x ) around ( x = a ), follow these steps:
- Step 1: Compute Derivatives - Find the derivatives of ( f(x) = \frac{1}{x} ) of all orders.
- Step 2: Evaluate at ( x = a ) - Substitute ( x = a ) into each derivative.
- Step 3: Construct the Series - Use the Taylor Series formula to write the infinite sum.
📘 Note: The Taylor Series for ( 1/x ) converges only for ( |x - a| < |a| ), so be mindful of the radius of convergence. (Radius of Convergence, Series Convergence)
The Formula: Taylor Series for 1/x

The Taylor Series for ( \frac{1}{x} ) around ( x = a ) is given by:
[ \frac{1}{x} = \frac{1}{a} \sum_{n=0}^{\infty} \left( \frac{a - x}{a} \right)^n ]This formula is valid for ( |x - a| < |a| ). (Mathematical Formulas, Series Representation)
Applications of the Taylor Series for 1/x

Understanding the Taylor Series for ( 1/x ) has practical applications in:
- Numerical Analysis - Approximating ( 1/x ) for specific values.
- Complex Analysis - Studying functions in the complex plane.
- Physics and Engineering - Solving problems involving inverses of variables.
| Derivative Order | Derivative of 1/x |
|---|---|
| 1st | -\frac{1}{x^2} |
| 2nd | \frac{2}{x^3} |
| 3rd | -\frac{6}{x^4} |

Checklist: Mastering the Taylor Series for 1/x

- Understand the Taylor Series formula.
- Compute derivatives of ( 1/x ) up to higher orders.
- Evaluate the series at a specific point ( a ).
- Apply the series in practical problems.
The Taylor Series for 1/x is a fascinating topic that bridges foundational calculus with advanced mathematics. By grasping its derivation and applications, you’ll gain a deeper understanding of function behavior and series expansions. Use this guide as a starting point to explore further into the world of infinite series and their real-world applications. (Advanced Mathematics, Function Behavior)
What is the Taylor Series used for?
+The Taylor Series is used to represent functions as infinite sums of their derivatives, enabling approximation and analysis of complex functions. (Function Approximation, Mathematical Analysis)
Why is the Taylor Series for 1/x important?
+It provides a way to express ( 1/x ) as an infinite series, which is useful in numerical analysis, complex analysis, and solving inverse-related problems. (Numerical Analysis, Complex Analysis)
What is the radius of convergence for the Taylor Series of 1/x?
+The series converges for ( |x - a| < |a| ), meaning it works within a specific interval around the center point ( a ). (Convergence Criteria, Interval of Convergence)



