Mastering Trigonometric Identities in Calculus 2

<!DOCTYPE html>
Trigonometric identities are a cornerstone of Calculus 2, providing essential tools for solving complex problems in integration, differentiation, and equation manipulation. Whether you’re a student preparing for exams or a professional refreshing your math skills, mastering these identities is crucial. This guide breaks down the key concepts, strategies, and practice techniques to help you confidently tackle trigonometric identities. (Calculus 2 tips, trigonometric identities, math study guide)
Understanding Trigonometric Identities
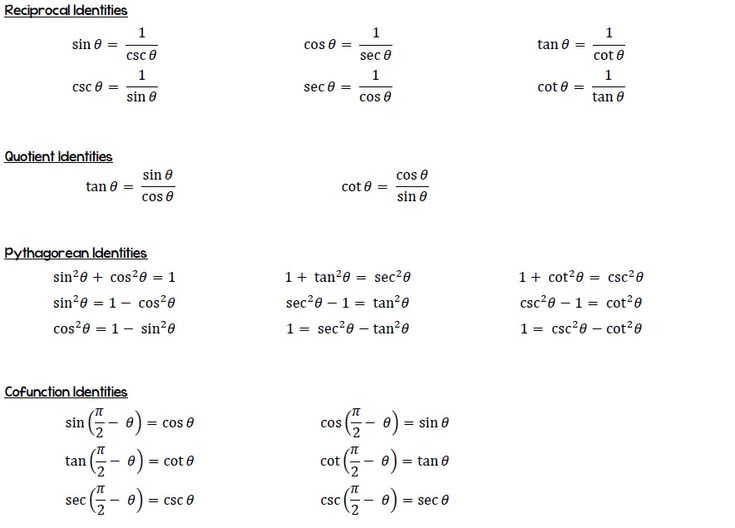
Trigonometric identities are equations involving trigonometric functions that hold true for all values of the variables within their domains. These identities are fundamental in simplifying expressions, solving equations, and evaluating integrals. Common identities include the Pythagorean identities, reciprocal identities, quotient identities, and co-function identities. (Trigonometric functions, Pythagorean identities, Calculus 2 basics)
Key Trigonometric Identities
- Pythagorean Identities: ( \sin^2(x) + \cos^2(x) = 1 )
- Reciprocal Identities: ( \csc(x) = \frac{1}{\sin(x)}, \sec(x) = \frac{1}{\cos(x)}, \cot(x) = \frac{1}{\tan(x)} )
- Quotient Identities: ( \tan(x) = \frac{\sin(x)}{\cos(x)}, \cot(x) = \frac{\cos(x)}{\sin(x)} )
Strategies for Mastering Trigonometric Identities

Mastering trigonometric identities requires a combination of memorization, practice, and strategic problem-solving. Here are some effective strategies to enhance your skills: (Math problem-solving, study strategies, Calculus 2 practice)
1. Memorize Fundamental Identities
Start by memorizing the basic trigonometric identities. Flashcards or repetition exercises can be helpful. Understanding the relationships between sine, cosine, and tangent will make it easier to derive other identities. (Memorization techniques, math flashcards)
2. Practice Regularly
Consistent practice is key to mastering trigonometric identities. Work through a variety of problems, starting with simple ones and gradually increasing the complexity. Online resources and textbooks offer plenty of practice questions. (Math practice, online resources)
📘 Note: Regular practice not only reinforces your memory but also helps you recognize patterns in trigonometric equations.
3. Use Visual Aids
Visual aids like the unit circle and graphs of trigonometric functions can provide intuitive insights into identities. Drawing diagrams or using graphing tools can make abstract concepts more tangible. (Unit circle, graphing tools)
Common Mistakes to Avoid

When working with trigonometric identities, students often make common mistakes that can lead to incorrect solutions. Being aware of these pitfalls can help you avoid them: (Common math mistakes, Calculus 2 errors)
- Forgetting Domain Restrictions: Always consider the domain of the trigonometric functions involved.
- Misapplying Identities: Ensure you apply identities correctly, especially when dealing with reciprocal and quotient identities.
- Overcomplicating Problems: Sometimes, simpler approaches like factoring or using basic identities can solve complex problems more efficiently.
Checklist for Mastering Trigonometric Identities

- Memorize key trigonometric identities.
- Practice regularly with diverse problems.
- Use visual aids to understand concepts better.
- Review common mistakes and avoid them.
- Test your knowledge with timed exercises.
By following these strategies and staying consistent in your practice, you’ll gain confidence in handling trigonometric identities in Calculus 2. Whether you’re preparing for exams or applying these concepts in real-world scenarios, a solid grasp of trigonometric identities will serve you well. (Calculus 2 mastery, math confidence, trigonometric identities)
What are the most important trigonometric identities to memorize?
+The most important identities include the Pythagorean identities, reciprocal identities, and quotient identities. These form the foundation for more complex manipulations. (Trigonometric identities, math memorization)
How can I improve my speed in solving trigonometric identity problems?
+Regular practice and recognizing patterns in problems can significantly improve your speed. Timed exercises can also help. (Math speed, problem-solving tips)
Are there any tools to help with trigonometric identities?
+Yes, graphing calculators and online tools like Desmos or Symbolab can assist in visualizing and verifying identities. (Graphing tools, online math tools)


