Examples of Quotient of Powers Simplified
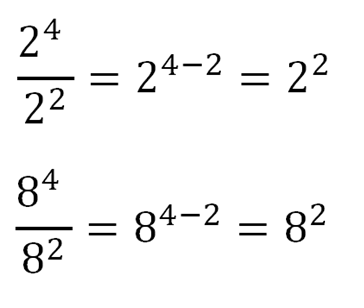
<!DOCTYPE html>
Understanding the quotient of powers is essential in algebra, especially when simplifying expressions involving exponents. This concept allows you to divide numbers or variables raised to certain powers efficiently. Whether you’re a student, educator, or professional, mastering this skill can save time and reduce errors in mathematical calculations. Below, we explore examples of the quotient of powers simplified, breaking down the process step by step.
What is the Quotient of Powers?

The quotient of powers rule states that when dividing two expressions with the same base, you subtract the exponent of the denominator from the exponent of the numerator. Mathematically, it is represented as: am / an = a(m-n). This rule simplifies complex expressions and is widely used in algebra, calculus, and other mathematical fields. (quotient rule, exponent rules, algebraic simplification)
Examples of Quotient of Powers Simplified

Example 1: Simplifying with Integer Exponents
Consider the expression x7 / x3. Using the quotient rule, subtract the exponents: x(7-3) = x4. This simplifies the expression to x4. (integer exponents, simplifying expressions)
Example 2: Simplifying with Variable Bases
For the expression y5 / y2, apply the quotient rule: y(5-2) = y3. The simplified form is y3. (variable bases, exponent subtraction)
Example 3: Simplifying with Negative Exponents
Simplify z-4 / z-2. Using the quotient rule, subtract the exponents: z(-4 - (-2)) = z-2. This simplifies to z-2, which can also be written as 1 / z2. (negative exponents, reciprocal form)
📘 Note: When dealing with negative exponents, remember that a-n = 1 / an. This is crucial for accurate simplification.
Practical Applications of Quotient of Powers

The quotient of powers rule is not just a theoretical concept; it has practical applications in various fields:
- Engineering: Simplifying equations for structural analysis.
- Physics: Reducing complex formulas in mechanics and electromagnetism.
- Economics: Modeling growth rates and financial projections.
Checklist for Simplifying Quotient of Powers

Follow these steps to simplify expressions using the quotient of powers rule:
- Identify the base and exponents in the numerator and denominator.
- Ensure the bases are the same; if not, the rule does not apply.
- Subtract the exponent of the denominator from the exponent of the numerator.
- Write the result with the base and the new exponent.
Mastering the quotient of powers rule enhances your ability to handle complex mathematical expressions efficiently. By practicing with various examples, you’ll gain confidence in applying this rule across different scenarios. (mathematical mastery, algebra practice)
What is the quotient of powers rule?
+The quotient of powers rule states that when dividing two expressions with the same base, you subtract the exponent of the denominator from the exponent of the numerator: am / an = a(m-n).
Can the quotient rule be applied to different bases?
+No, the quotient rule only applies when the bases of the expressions are the same.
How do negative exponents affect the quotient rule?
+Negative exponents are handled the same way as positive exponents in the quotient rule. Subtract the exponents as usual, and if the result is negative, express it as a reciprocal.



