Trapezoidal Rule Solver: Fast, Accurate Numerical Integration

<!DOCTYPE html>
Numerical integration is a cornerstone of computational mathematics, enabling the approximation of definite integrals for functions where analytical solutions are impractical or impossible. Among the various methods available, the Trapezoidal Rule stands out for its simplicity and efficiency. Whether you're a student, researcher, or professional, understanding and utilizing a Trapezoidal Rule Solver can significantly streamline your workflow. This post explores the method, its applications, and how to leverage it for fast and accurate results.
What is the Trapezoidal Rule?

The Trapezoidal Rule is a numerical integration technique that approximates the definite integral of a function by dividing the area under the curve into trapezoids. It’s particularly useful for functions with smooth, continuous curves. The formula for the Trapezoidal Rule is:
∫ab f(x) dx ≈ (h/2) [f(a) + 2∑i=1n-1 f(xi) + f(b)]
Where:
- a and b are the limits of integration,
- h is the width of each trapezoid (step size),
- n is the number of trapezoids.
📘 Note: The accuracy of the Trapezoidal Rule improves with smaller step sizes (larger n), but computational cost increases.
Why Use a Trapezoidal Rule Solver?

A Trapezoidal Rule Solver automates the process, saving time and reducing errors. Here’s why it’s a preferred choice:
- Speed: Quickly computes integrals for large datasets.
- Accuracy: Provides reliable results for smooth functions.
- Simplicity: Easy to implement and understand.
Applications of the Trapezoidal Rule

The Trapezoidal Rule is widely used in various fields, including:
| Field | Application |
|---|---|
| Physics | Calculating areas under velocity-time graphs |
| Engineering | Estimating work done by variable forces |
| Economics | Computing consumer surplus |

How to Implement a Trapezoidal Rule Solver
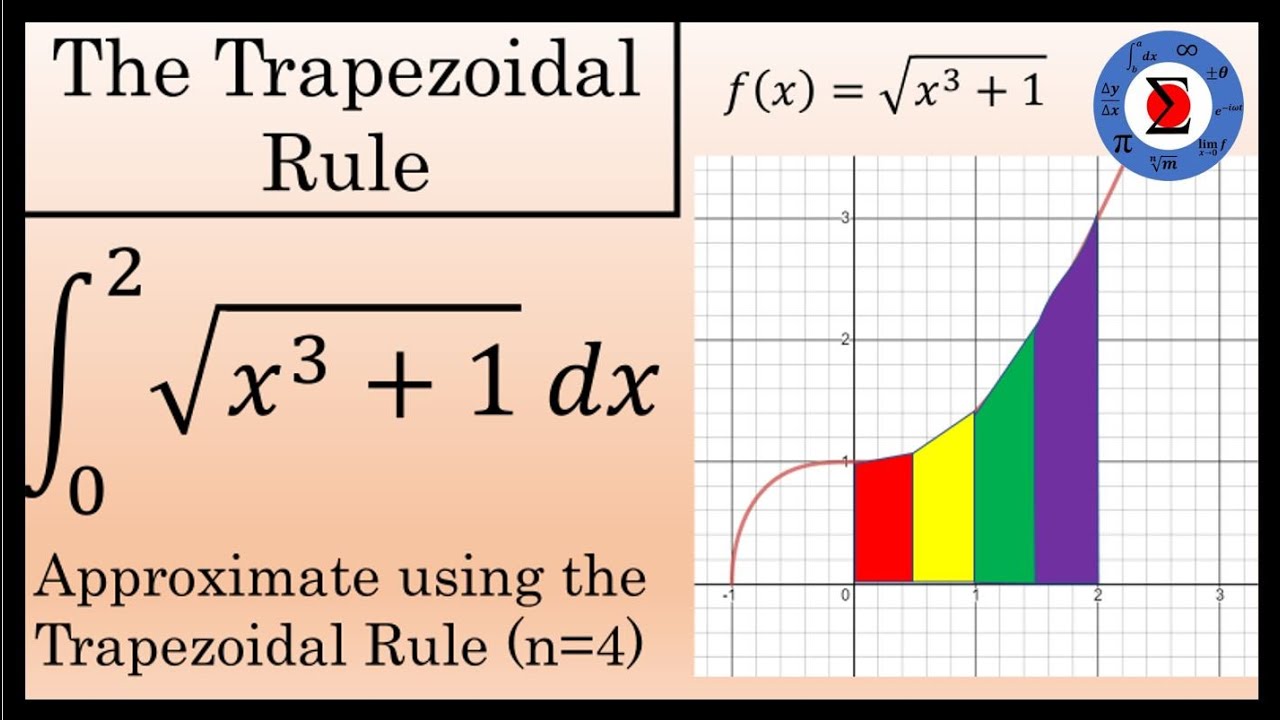
Implementing a Trapezoidal Rule Solver involves the following steps:
- Define the Function: Input the function f(x) to be integrated.
- Set Limits: Specify the integration limits a and b.
- Choose Step Size: Determine the number of trapezoids (n) or step size (h).
- Compute the Integral: Apply the Trapezoidal Rule formula.
📌 Note: For optimal results, balance accuracy and computational efficiency by adjusting n or h.
Choosing the Right Trapezoidal Rule Solver

When selecting a Trapezoidal Rule Solver, consider the following:
- Ease of Use: Look for user-friendly interfaces or libraries.
- Performance: Ensure it handles large datasets efficiently.
- Accuracy: Verify its precision for your specific use case.
For commercial applications, prioritize solvers with advanced features like parallel processing or cloud integration,numerical integration tools,mathematical software,computational efficiency.
The Trapezoidal Rule Solver is an invaluable tool for anyone dealing with numerical integration. Its simplicity, speed, and accuracy make it suitable for a wide range of applications. By understanding its principles and leveraging the right tools, you can tackle complex integrals with ease. Whether you're a beginner or an expert, incorporating a Trapezoidal Rule Solver into your workflow can significantly enhance productivity and precision.
What is the Trapezoidal Rule used for?
+The Trapezoidal Rule is used to approximate the definite integral of a function by dividing the area under the curve into trapezoids. It’s commonly applied in physics, engineering, and economics.
How accurate is the Trapezoidal Rule?
+The accuracy of the Trapezoidal Rule depends on the step size (h) and the smoothness of the function. Smaller step sizes yield more accurate results but increase computational cost.
Can the Trapezoidal Rule handle discontinuous functions?
+The Trapezoidal Rule is best suited for continuous, smooth functions. For discontinuous functions, other methods like Simpson's Rule may be more appropriate.

